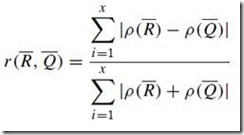A Cluster Pattern Algorithm for the Analysis of Multiparametric Cell Assays

The issue of multiparametric analysis of complex single cell assays of both static and flow cytometry (SC and FC, respectively) has become common in recent years. In such assays, the analysis of changes, applying common statistical parameters and tests, often fails to detect significant differences between the investigated samples. The cluster pattern similarity (CPS) measure between two sets of gated clusters is based on computing the difference between their density distribution functions set points. The CPS was applied for the discrimination between two observations in a four-dimensional parameter space. The similarity coefficient (r) ranges between 0 (perfect similarity) to 1 (dissimilar). Three CPS validation tests were carried out: on the same stock samples of fluorescent beads, yielding very low r (0, 0.066); and on two cell models: mitogenic stimulation of peripheral blood mononuclear cells (PBMC), and apoptosis induction in Jurkat T cell line by H2O2. In both latter cases, r indicated similarity (r < 0.23) within the same group, and dissimilarity (r > 0.48) otherwise. This classification and algorithm approach offers a measure of similarity between samples. It relies on the multidimensional pattern of the sample parameters. The algorithm ompensates for environmental drifts in this apparatus and assay; it also may be applied to more than four dimensions.

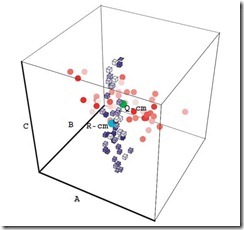
This diagram illustrating two sampled datasets R and Q in such a four-dimensional Euclidean space. To bring the two datasets, R and Q (Fig. 2a), to a common ground, their mass centers are translated to the axes origin, point O = (0, 0, 0, 0) (Fig. 2b); thereafter, the datasets are termed as R and Q, respectively. Let ρ(R) and ρ(Q) be the density distributions of points belonging to the bounded sets R and Q in space E4. Then we define a pattern similarity coefficient r(R, Q) as the integral over the E4 space of the absolute values of the density differences:

As it can be seen, in this Equation, the similarity coefficient has the following properties:

1. 0 ‹ r ‹ 1,

2. if R = Q, then r = 0,

3. r(R, Q) = r(Q, R).

The element dE4 in the E4 space must have a finite size. Thus, in its discrete mode, the Eeuation is expressed as:

where x is the number of dE4 elements (bins) in E4.

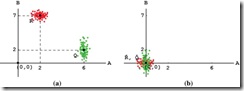
The Translation of R and Q sample patterns center of mass to the origin is shone in the next image. (a) An example of a scatter diagram showing synthetic data of two parametric clusters R (red) and Q (green). (b) Clusters R and Q, after normalization and translation of their mass centers to the origin, are overlaid on each other and become R and Q, respectively. The large black dots mark the mass centers of the clusters.